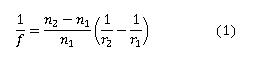
n₂ is the index of refraction of the lens, n₁ is the index of refraction of the surrounding medium, r₁ is the radius of curvature of the incoming surface, and r₂ is the radius of curvature of the exiting surface, and f is the focal length.  For our application the second surface is flat (ie r₂=infinity).  This simplifies the equation to equation 2.

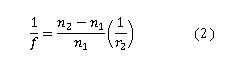
solving for the focal length f we get equation 3

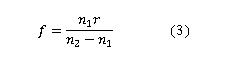
Notice that the subscript from the radius since we only have one curved surface, and that the negative sign was incorporated into the difference of the index of refraction term thats in the denominator of equation 3.  Now that we have the focal length equation that we want, what can it tell us about lenses.  Notice that the only variables are r and f, the refractive indexes are constant.  So the focal length varies directly with the radius of curvature!!! If the radius were to get larger, the focal length gets larger, and if the radius of curvature gets smaller, so too does the focal length.  Equation 3 shows that a variable focusing lens can be made only if we can vary the radius (or index of refraction, but it is hard and not practical).  Now on to how to change the radius although you might already guess how.

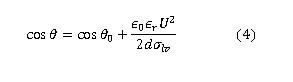
α is the new contact angle with the applied electric potential U. α₀ is the equilibium contact angle when there is no applied voltage, d is the thickness of the dielectric layer that sits between the drop and the electrode, ε_d is the permittivity of the dielectric film.  Sigma is the surface energy of the surface between the liquid and the external medium.  Equation 4 is important because it tells us how the contact angle changes with applied voltage. 

 

At this point you may be asking yourself "okay, but how does the radius change with applied voltage?"  From the depths of the mathematics handbook [2]  an equation for the volume of a spherical cap is found.  A spherical cap is a shape that comes from chopping the top off of a sphere.  One assumption that was made, was that the volume of the droplet is small enough so that the droplet is a perfect section of a sphere.  The volume can be written as Equation 5.

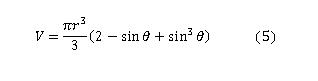
In Equation 5, V is the volume of the droplet, r is the radius of curvature, and alpha is the contact angle that we can find using Equation 4.  Solving Equation 5 for the radius we get equation 6 where R is the radius of curvature from equation 5, r.

Substituting Equation 6 into Equation 3 we get an equation for the focal length as a function of the contact angle (Equation 7).